鐵電氧化鉿鋯（HZO）：開啟下世代節能晶片與能源應用之鑰

氧化鉿鋯憑藉優異鐵電性與 CMOS 相容性，成為新世代節能關鍵。本文深入剖析其物理機制，並探討能源採集領域之應用。（資料來源：閎康科技，原文為〈節能鐵電氧化鉿鋯於能源領域理論與應用〉，本文出自國立臺灣大學重點科技研究學院李敏鴻教授、巫冠霆碩士生、劉呈宏博士生團隊，經科技新報編修為上下兩篇，此篇為上篇。）

▲ 本文出自國立臺灣大學重點科技研究學院李敏鴻教授、巫冠霆碩士生、劉呈宏博士生團隊，經科技新報編修。

氧化鉿 (HfO₂) 薄膜系統的鐵電性（Ferroelectricity) 來源

2011 年 T. S. Böscke 首次發表 Si 摻雜 HfO₂ 薄膜中的鐵電（ferroelectric, FE）和反鐵電（antiferroelectric, AFE），如圖 1。他提出氧化鉿鐵電相為正交晶相 (orthorhombic phase) ，是從四方晶相 (tetragonal phase) 冷卻過程中轉變而成，如圖 2 ^[1]。

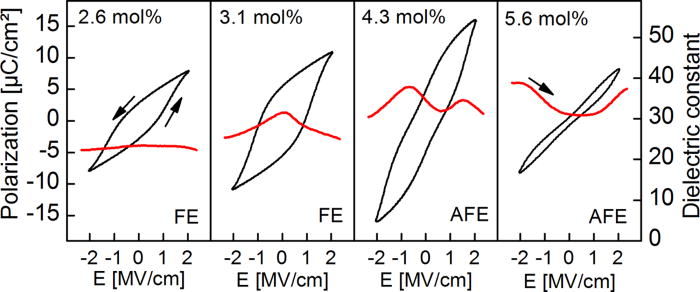
▲ 圖 1 不同的Si 摻雜濃度的電容與電滯曲線 ^[1]

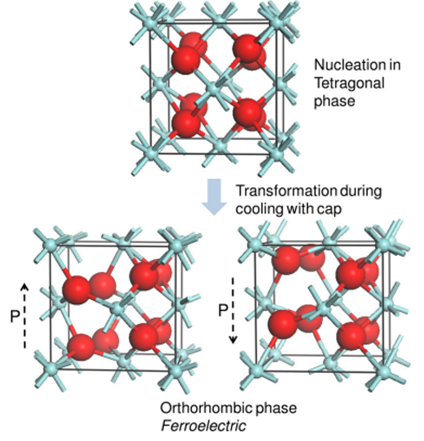
▲ 圖 2 四方晶相轉變為正交晶相以及不同鐵電相的極化狀態示意圖 ^[1]

HfO₂ 基材料之鐵電／反鐵電行為與摻雜效應

自從在 HfO₂ 基系統中發現了這些特性後，相關研究應用迅速展開。後續研究發現 HfO₂ 基材料中的鐵性歸因源於非中心對稱的正交晶相 (Pca2₁) 的形成^[2]，且 HfO₂ 中的鐵電特性可由多種摻雜物誘導，例如矽 (Si)、鋁 (Al)、鈣  (Ca)、釔 (Y)、鍶 (Sr)、鎦 (Lu)、釓 (Gd) 和鑭 (La)，以及 HfO₂-ZrO₂ 的固態溶解和未摻雜的 HfO₂。

然而，與鐵電行為相較，HfO₂ 基材料的反鐵電性只能由較有限的摻雜組合生成，例如鋁 (Al)、矽 (Si) 以及 HfO₂-ZrO₂ 的固態溶解，或者鋁 (Al)、矽 (Si) 摻雜進 Hf₀.₅Zr₀.₅O₂。HfO₂ 基材料反鐵電特性可歸因於電場誘導的非極性四方晶相（P4₂/nmc）和極性正交晶相（Pca2₁）之間的相變，從而形成雙迴圈電滯(hysteresis) 曲線^[3]。

Zr 摻雜比例對 HfO₂ 鐵電性的影響

2012 年，J. Müller 團隊發表了 Zr 摻雜 HfO₂ 的研究成果 ^[4]，並指出 Zr 在材料中的含量會顯著影響其鐵電行為。為精確控制 Hf 與 Zr 的比例，文獻採用原子層沉積（Atomic Layer Deposition, ALD）技術進行薄膜製備。圖 3 顯示不同 Zr 含量下的電滯曲線與介電常數隨電場變化的行為：當 Zr 的摻雜濃度低於 Hf（x < 0.5）時，材料呈現鐵電性，且隨著 Zr 含量增加，介電常數亦同步提升；而當 Zr 的濃度高於 Hf（x > 0.5）時，電滯曲線則轉為反鐵電特性。

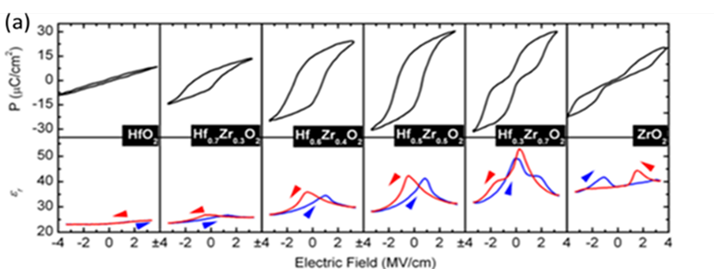
▲ 圖 3  不同 Zr 比例的極化量和介電常數對電場關係圖 ^[4]

鐵電材料的點群晶體結構與壓電、熱電、鐵電特性

鐵電性材料僅能存在於缺乏反轉中心（inversion center）的晶體中，也就是非中心對稱的結構。在 32 種晶體點群（crystal point groups）中，雖然全部皆具備介電性，但只有其中 21 種為非中心對稱點群。其中再有 20 種具備壓電性（點群 432 因具有額外對稱元素，使壓電響應相互抵消而被排除），此類材料即為壓電（piezoelectric）材料。

在這些壓電點群中，只有 10 種能形成永久電偶極矩（permanent dipole），此特性稱為自發極化（spontaneous polarization），這電荷量可隨溫度變化而均勻調整，為熱電（pyroelectric）材料。雖然目前沒有明確的晶體學分類能完全區分熱電與鐵電材料。一般的判定方式為：若材料具永久電偶極矩，偶極可在低於崩潰電場（breakdown field）的條件下被重新轉向，則可歸類為鐵電材料。

綜合來說，所有鐵電材料必然具有熱電性與壓電性，但反之並非所有熱電或壓電材料皆具備鐵電性。具備鐵電、熱電與壓電性的點群分布如圖 4 ^[5]，而階層分類則如圖 5 ^[6]。

▲ 圖 4 具有鐵電性、熱電性和壓電性的點群 ^[5]

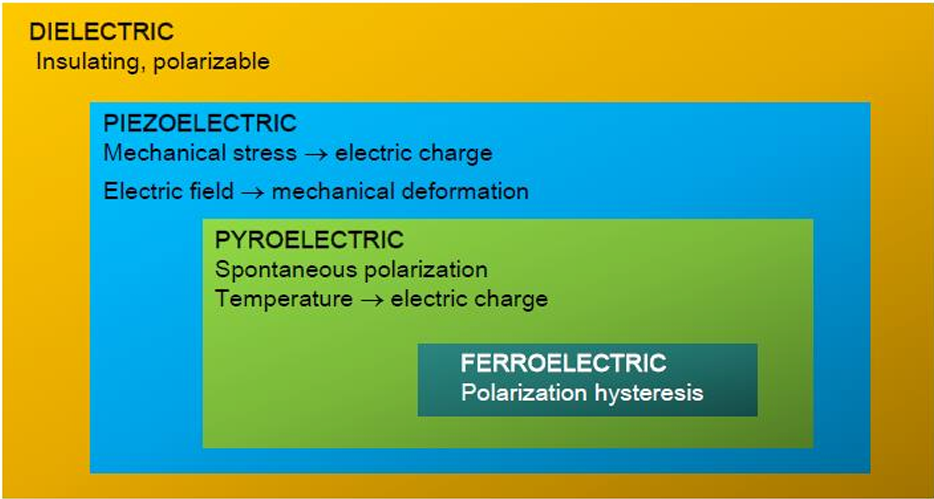
▲ 圖 5 鐵電性、熱電性和壓電性的階層分類 ^[6]

鐵電材料的熱電、機械與電耦合及能源應用

由於鐵電材料的晶體結構特性，它能夠在電、熱與機械變量之間實現熱力學上的可逆耦合，如圖 6 。因此，在接近相變時，這些熱力學過程可能並非可逆^[7][8]。

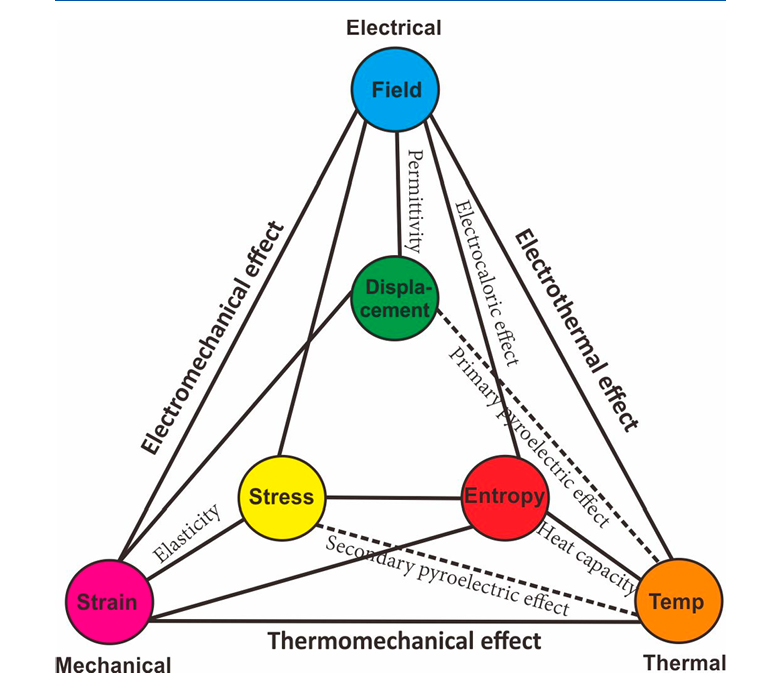
▲ 圖 6 Heckmann 圖顯示電、熱和機械性能之間的相互作用 ^[9]。

在圖 6 中外圍的圓分別表示代表外部對於材料的驅動力：電場 (Field)、溫度 (Temp) 和機械應力 (strain)；內部的圓分別表示為材料內部的響應：電位移 (Displacement)、熵 (Entropy) 和應變 (Stress) ^[9]。連接兩個圓的線表示變量間的耦合——當其中一個變量改變時，會引起另一個變量的響應。在各種廢熱來源中，電子元件比重不斷增加，也導致能源消耗大幅增加。如果能將廢熱回收作為電力來源重新利用，再生利用與高能耗晶片整合將可帶來重大能源效率的改善。基於鐵電 HfO₂ 材料在電性（electrical property）與熱性（thermal property）之間的耦合（coupling），材料在能源儲存、熱電能源收集以及電卡（electrocaloric）製冷等應用中展現出極大潛力，如圖 7 ^[10]。

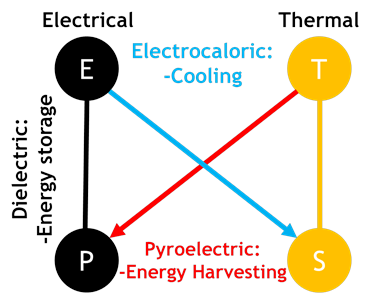
▲ 圖 7 電和熱特性關係之耦合，顯示不同交互作用下的效應，包含能源儲存、能源收集、固態製冷^[10]。

靜電電容於能源儲存的應用

D. Zhou 團隊於 2020 年 ACS Energy Materials 期刊^[11] 整理過往文獻，歸納所有出類型的線性和非線性介質材料典型極化行為，包含順電 (Paraelectric, PE)、線性 (Linear, LE)、FE、鬆弛鐵電 (Relaxor FE, ReFE) 和AFE ^[12-14]。

• LE：隨外部電場的電位移呈線性比例變化如圖 8 (a)。

• PE：可以在外加電場下極化，但是當電場消失時，材料會回歸非極性狀態如圖8 (b)。

• FE：則是在無外加電場亦能展現極化，具有較寬的電滯曲線如圖8 (c)。

• ReFE：極化的極化域 (Domain) 大大降低FE domain之間的相互耦合，其有限的自發極化導致收縮的電滯曲線如圖 8 (d)。

• AFE：則是展現雙迴圈之電滯曲線如圖 8 (e)。

電場和極化之間的交互作用可用於電荷儲存現象，圖 9 顯示 AFE 的儲能密度(energy-storage density, ESD) 和能源損失 (Energy loss)。在充電過程中，能源被儲存在靜電電容中，如藍色和綠色區域；放電過程中，釋放出可獲得的 ESD，如綠色區域所示。透過極化 – 電場電滯迴圈中充／放電 (charge/discharge) 封閉曲線與極化軸之間封閉面積的加總，可計算介電材料的總能源 E_total​^[8]。

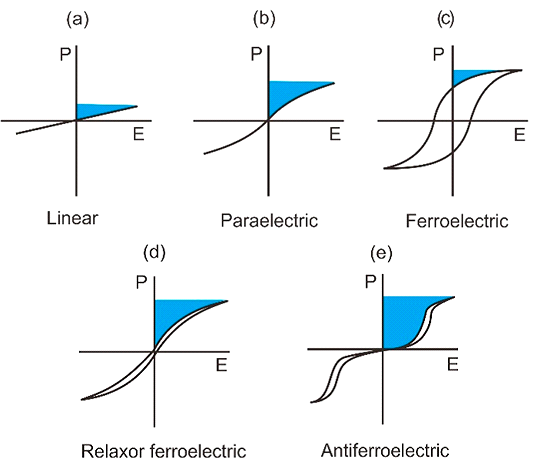
▲ 圖 8 極化電場曲線於不同類型介電材料的表現，曲線上方的藍色區域為儲能密度^[12-14]。

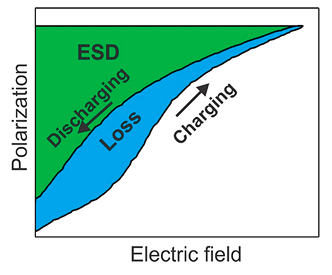
▲ 圖 9 對於靜電電容的極化電場作用中，電滯曲線與能源儲存密度、損失的關係^[11]。

能源收集機制與 Olsen Cycle

C. Mart 團隊於2020 年 IEEE International Electron Devices Meeting (IEDM) 研討會^[15]中指出，熱電 (pyroelectric) 材料可應用於回收部分耗散功率，將廢熱轉化為電力，如圖 10 。電滯曲線展現與溫度具有相關性的熱電效應。根據熱力學(thermodynamics)原理，溫度會影響鐵電材料在穩定態下自由能 (free energy) 不同相態之間的能障 (barrier)^[16]隨著溫度升高，會引起相變化，鐵電正交相 (orthorhombic) 轉變為四方相 (tetragonal)，導致殘餘極化量降低。

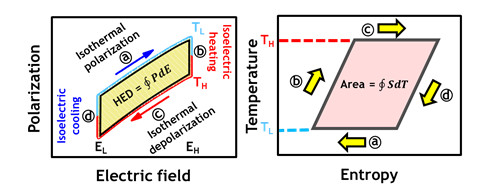
Olsen 團隊利用固態極性材料於熱電^[17]，提出奧森循環 (Olsen cycle) 將熱能轉化電能，如圖11(a)的極化-電場圖 (P-E diagram)，此過程包含四個連續的步驟：

ⓐ等溫極化(Isothermal polarization)：於較低溫的環境下外加電場使其極 (poling)

ⓑ等電場加熱(Isoelectric heating)：於加熱的過程中發生部分的去極化 (depoling) 現象

ⓒ等溫去極化(Isothermal depolarization)：於較高溫的環境下減少外加電場使去極化

ⓓ 等電場冷卻(Isoelectric cooling)：於降溫的過程中發生部分的極化現象

以及圖 11 (b)系統上對應的溫度 – 熵圖 (T-S diagram)：

ⓐ熵放出(Entropy ejection)

ⓑ熱能吸收(Heat absorption)

ⓒ熵吸收(Entropy absorption)

ⓓ 熱能放出(Heat ejection)

熱電材料的極化/去極化現象指的是系統上熵或熱的放出/吸收，從圖11 (b) 的等溫可逆過程中可以經由熵變化 (ΔS) 和溫度 (T) 乘積計算熱量大小，HED 是可收集的能源密度 (Harvestable Energy Density)，E_H 是高外加電場，E_L 是低外加電場，T_L 是相對低溫環境，T_H 是相對高溫環境，因此經過單次 Olsen cycle 循環的情況，吸收的熱量 (T_HΔS) 大於釋放的熱量 (T_LΔS)，代表所吸收的熱量可轉換成電能。具備高效的熱電能源收集所需的條件如下：

(i) 越大的可收集能源密度 (HED)，(ii) 無鉛性質，(iii) 奈米薄膜結構，(iv) 高熔點，以及 (v) 崩潰電壓　(Breakdown voltage)。螢石型結構的鐵電材料如 HZO，是非含鉛，且可以在奈米薄膜中展現出鐵電性，以及具有較寬廣的相變化程度、高較大的能隙 (Band gap) ~ 5.5 eV，高崩潰電場，為熱電材料候選者。

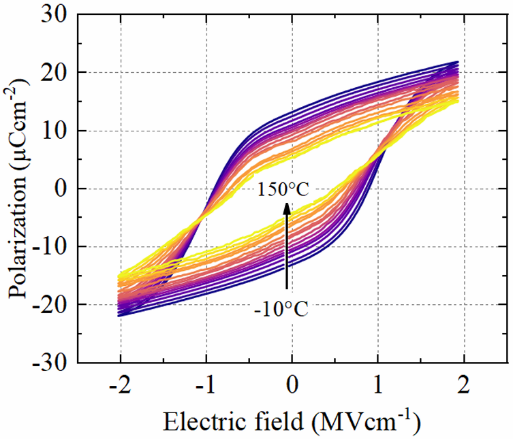
▲ 圖 10 極化電場關係中，熱電效應導致電滯曲線改變 ^[15] 。

▲ 圖 11 (a) 極化電場關係說明奧森循環 (Olsen cycle) (b) 循環過程各步驟相對應溫度熵的關係 ^[17]。

電卡與負電卡效應：HZO 製冷行為的物理基礎

M.-H. Park 團隊於 2016 年 Advanced Material 期刊中 ^[18] 中提出鐵電氧化鉿鋯 (Hf_1-xZr_xO₂) 薄膜用於製冷材料的概念，其中電卡降溫效應 (electrocaloric effect, ECE) 的重要參數為溫度變化 (ΔT) 和熵變化 (ΔS)，取決於 (∂P/∂T)_E 變化，即為圖 12 之固定電場下極化-溫度的變化量 (斜率)，結果呈現於圖 13 (a) 與 (b)。不同濃度的氧化鉿鋯所計算出的 ΔT 和 ΔS。當斜率為負時，熵會隨著電場增加而下降，材料釋放熱量並達到冷卻的效果，而此種現象於先前提到的 Olsen cycle 正好相反，又稱為Inverse-Olsen cycle。反之當斜率為正時，熵會隨著電場增加而上升，材料吸收熱量並達到升溫 (環境冷卻) 的效果，此現象效果類似於 Olsen cycle，又稱為負電卡效應(Negative Electrocaloric Effect)。並計算得知製冷能力 RC (Refrigerant Capacity)，如圖13(c)。
目前仍未有明確且完美理論模型說明氧化鉿鋯薄膜中鐵電與反鐵電的電卡和負電卡效應，但是鐵電材料於先進製程技術的冷卻應用中具有高度的可行性，甚至結合正負電卡效應達到循環冷卻的效果。

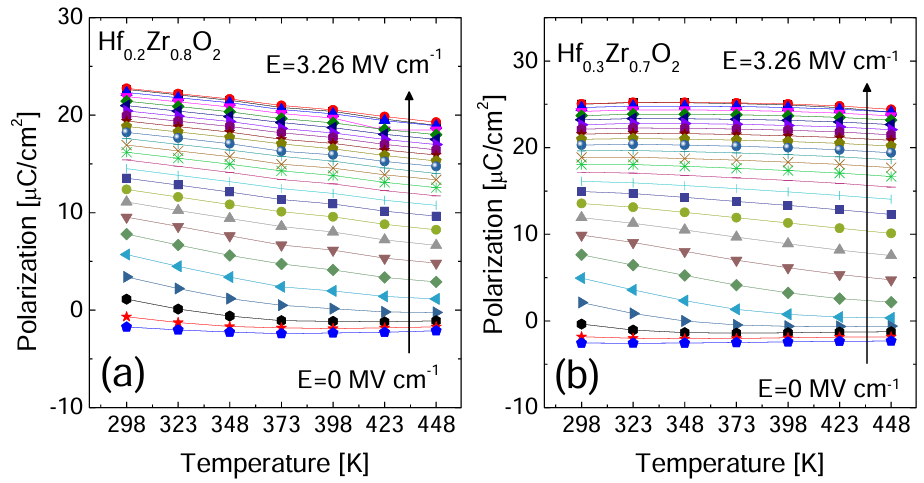
▲ 圖 12 氧化鉿鋯薄膜隨著溫度變化的極化量，(a) Hf_0.2Zr_0.8O₂, (b) Hf_0.3Zr_0.7O₂，顯示極化作為溫度的函數下其斜率為負值^[18]。

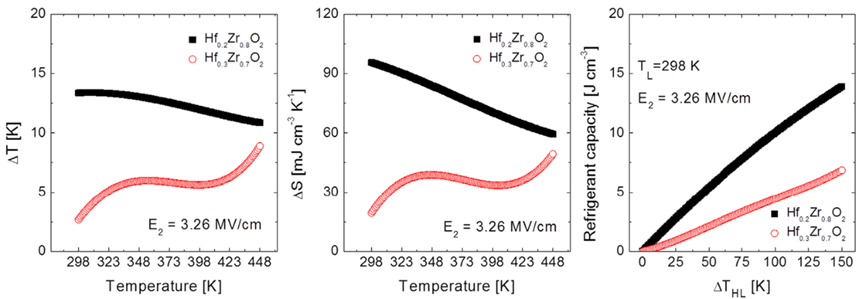
▲ 圖 13 圖 12 之數據萃取：(a)溫度變化 (ΔT) 和 (b) 熵變化 (ΔS)，並計算 (c) 製冷能力RC (Refrigerant Capacity)。^[18]

（資料來源：閎康科技；首圖：Shutterstock）

延伸閱讀：鐵電氧化鉿鋯（HZO）：打造下一代晶片冷卻與熱管理技術的關鍵材料

References：

[1] T. S. Böscke et al., Appl. Phys. Lett. 99, 102903 (2011)

[2] X. Sang et al., Appl. Phys. Lett. 106, 162905 (2015)

[3] R. Materlik et al., J. Appl. Phys. 117, 134109 (2015)

[4] J. Müller et al., Nano Lett. 12, 8, 4318–4323 (2012)

[5] U. Schroeder et al., Duxford: Woodhead Publishing, First edition, (2019)

[6] T. Mikolajick et al., IEEE IEDM. Short course 2 (2017)

[7] S. G. Lu et al., Appl. Phys. Lett. 97, 202901 (2010)

[8] X. Li et al., J. Mater. Chem. C 1 (1), 23−37. (2013)

[9] F. Ali et al., ACS Appl. Electron. Mater. 2, 8, 2301–2317 (2020)

[10]  M. H. Park et al., Nano Energy, 12, 131–140 (2015)

[11]  F. Ali et al., ACS Appl. Energy Mater. 3, 7, 6036–6055 (2020)

[12]  Z. Yao et al., Adv. Mater. 29, 1601727 (2017)

[13]  R. Su et al., Polymer, 53, 728−739, (2012)

[14]  S. Tong et al., ACS Appl. Mater. Interfaces 5, 4, 1474–1480 (2013)

[15]  C. Mart et al., IEEE IEDM, 561 (2020)

[16]  M. H. Park et al., Phys. Status Solidi RRL 13, 1900177 (2019)

[17]  R. B. Olsen et al., J. Appl. Phys. 58, 4709–4716 (1985)

[18]  M. H. Park et al., Adv. Mater. 28, 7956–7961 (2016)

[19] B. Ma et al., J. Mater. Res. 24, 2993 (2009)

[20] J. Li et al., J. Mater. Chem. 22, 23468–23476 (2012)

[21] M. H. Park et al., Adv. Ene. Mater. 4, 1400610 (2014)

[22] M. Pešic´et al., Adv. Funct. Mater. 26, 7486–7494 (2016)

[23] Y. He et al., Nanoscale Adv. 4, 4648-4657 (2022)

[24] K. D. Kim et al., Nano Energy 39, 390-399 (2017)

[25] C. Mart et al., Appl. Phys. Lett. 113, 122901 (2018)

[26] C. B. Vining et al., Nat. Mater. 8, 83-85 (2009)

[27] C. H. Liu et al., IEEE IEDM, 27-4 (2024)